Esses dias resolvi retomar o conhecimento de cálculo numérico que tive na faculdade. O primeiro tópico que abordei foi os métodos iterativos de obter zeros reais de funções. Tomei como base o livro de Cálculo Numérico que tive na faculdade.
Alguns desses métodos utilizam o Teorema de Bolzano que é um caso específico do Teorema do Valor Intermediário para garantir que existe uma raiz dado um determinado intervalo e com isso desenvolvem técnicas para encontrar ess raiz. De maneira simplificada, o Teorema de Bolzano diz que se uma função assume valor negativo para um determinado ponto 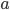 e um valor positivo para um determinado ponto
e um valor positivo para um determinado ponto 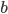 (ou vice versa, positivo pra
(ou vice versa, positivo pra 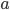 e negativo pra
e negativo pra 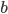 ), vai existir pelo menos uma raíz entre esse intervalo se a função for contínua. Isto é: Se
), vai existir pelo menos uma raíz entre esse intervalo se a função for contínua. Isto é: Se 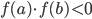 , existe raiz real. Veja a seguinte função:
, existe raiz real. Veja a seguinte função: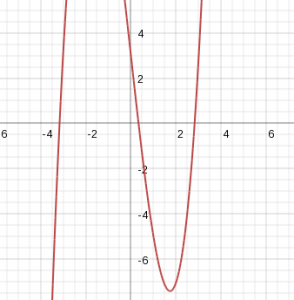
Seja o intervalo 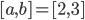 , para o valor de
, para o valor de 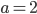 ,
, 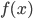 assume valor negativo e para
assume valor negativo e para 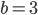 ,
, 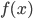 assume valor positivo, portanto,
assume valor positivo, portanto, 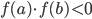 e pelo gráfico podemos ver que existe um valor entre
e pelo gráfico podemos ver que existe um valor entre 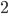 e
e 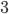 que é raíz dessa função. Nesse exemplo a função é
que é raíz dessa função. Nesse exemplo a função é 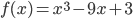 . Aplicando valores reais:
. Aplicando valores reais: 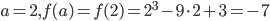 e
e 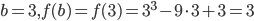 , então
, então 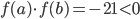 . Portanto, existe raiz entre
. Portanto, existe raiz entre 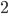 e
e 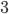 para a função
para a função 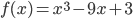 .
.
Com isso em mente, nesse tópico vamos abordar um método para encontrar esse raiz: o método da bissecção. Esse método consiste em tentar achar uma raiz em um intervalo subdividindo esse intervalo em duas metades a cada iteração, utilizando o teorema de Bolzano para verificar em qual metade está a raiz até atingir a precisão requerida. É um método simples, mas não necessariamente eficiente. Abaixo temos o código para esse método:
for (long k = 0; k < maxIter; k++) {
// x = (a + b)/2
BigDecimal x = a.add(b).divide(CommonValues.TWO.getValue());
// (b - a) < precision
if (b.subtract(a).compareTo(precision) < 0) {
// result a or b is ok too
return x;
}
// m = f(a)
BigDecimal m = f.evaluate(a);
// m*f(x) > 0
if (m.multiply(f.evaluate(x)).compareTo(BigDecimal.ZERO) > 0) {
a = x;
} else {
b = x;
}
}
Dado um intervalo 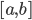 , na linha 4 dividimos o nosso intervalor na metade, na linha 7 verificamos se já atingimos a precisão alvo, se sim, retornamos um valor entre o intervalo
, na linha 4 dividimos o nosso intervalor na metade, na linha 7 verificamos se já atingimos a precisão alvo, se sim, retornamos um valor entre o intervalo 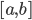 (linha 9). Caso contrário, aplicamos o teorema de bolzano:
(linha 9). Caso contrário, aplicamos o teorema de bolzano: 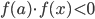 (linha 13 e 16) para verificar se a raiz está entre
(linha 13 e 16) para verificar se a raiz está entre 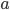 e
e 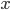 ou
ou 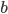 e
e 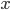 . Mudamos o intervalo de acordo com essa condição (linha 17 ou 19) e continuamos nesse loop (linha 1), até atingir a precisão correta (linha 7) ou até um determinado número de iterações (linha 1).
. Mudamos o intervalo de acordo com essa condição (linha 17 ou 19) e continuamos nesse loop (linha 1), até atingir a precisão correta (linha 7) ou até um determinado número de iterações (linha 1).
Como esse método é simples e previsível (sempre divisões ao meio) fica fácil calcular o número de iterações necessárias para ele encontrar a raiz dada uma precisão:
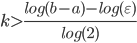
Onde 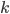 é o número de iterações e
é o número de iterações e 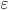 é a precisão desejada. O código para esse método e exemplos de execução encontram-se nos seguintes endereços: Github e Google Code.
é a precisão desejada. O código para esse método e exemplos de execução encontram-se nos seguintes endereços: Github e Google Code.